What Is a Fluid?

What Is a Fluid?

You will recall from physics that a substance exists in three primary phases: solid, liquid, and gas. (At very high temperatures, it also exists as plasma.) A substance in the liquid or gas phase is referred to as a fluid. Distinction between a solid and a fluid is made on the basis of the substance’s ability to resist an applied shear (or tangential) stress that tends to change its shape. A solid can resist an applied shear stress by deforming, whereas a fluid deforms continuously under the influence of a shear stress, no matter how small. In solids, stress is proportional to strain, but in fluids, stress is proportional to strain rate. When a constant shear force is applied, a solid eventually stops deforming at some fixed strain angle, whereas a fluid never stops deforming and approaches a constant rate of strain. 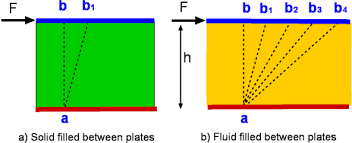Consider a rectangular rubber block tightly placed between two plates. As the upper plate is pulled with a force F while the lower plate is held fixed, the rubber block deforms, as shown in Fig. 1–2. The angle of deformation a (called the shear strain or angular displacement) increases in proportion to the applied force F. Assuming there is no slip between the rubber and the plates, the upper surface of the rubber is displaced by an amount equal to the displacement of the upper plate while the lower surface remains stationary. In equilibrium, the net force acting on the upper plate in the horizontal direction must be zero, and thus a force equal and opposite to F must be acting on the plate. This opposing force that develops at the plate–rubber interface due to friction is expressed as F 5 tA, where t is the shear stress and A is the contact area between the upper plate and the rubber. When the force is removed, the rubber returns to its original position. This phenomenon would also be observed with other solids such as a steel block provided that the applied force does not exceed the elastic range. If this experiment were repeated with a fluid (with two large parallel plates placed in a large body of water, for example),

the fluid layer in contact with the upper plate would move with the plate continuously at the velocity of the plate no matter how small the force F. The fluid velocity would decrease with depth because of friction between fluid layers, reaching zero at the lower plate. You will recall from statics that stress is defined as force per unit area and is determined by dividing the force by the area upon which it acts. The normal component of a force acting on a surface per unit area is called the normal stress, and the tangential component of a force acting on a surface per unit area is called shear stress (Fig. 1–3). In a fluid at rest, the normal stress is called pressure. A fluid at rest is at a state of zero shear stress. When the walls are removed or a liquid container is tilted, a shear develops as the liquid moves to re-establish a horizontal free surface. In a liquid, groups of molecules can move relative to each other, but the volume remains relatively constant because of the strong cohesive forces between the molecules. As a result, a liquid takes the shape of the container it is in, and it forms a free surface in a larger container in a gravitational field. A gas, on the other hand, expands until it encounters the walls of the container and fills the entire available space. This is because the gas molecules are widely spaced, and the cohesive forces between them are very small. Unlike liquids, a gas in an open container cannot form a free surface (Fig. 1–4). Although solids and fluids are easily distinguished in most cases, this distinction is not so clear in some borderline cases. For example, asphalt appears and behaves as a solid since it resists shear stress for short periods of time. When these forces are exerted over extended periods of time, however, the asphalt deforms slowly, behaving as a fluid. Some plastics, lead, and slurry mixtures exhibit similar behavior. Such borderline cases are beyond the scope of this text. The fluids we deal with in this text will be clearly recognizable as fluids. Intermolecular bonds are strongest in solids and weakest in gases. One reason is that molecules in solids are closely packed together, whereas in gases they are separated by relatively large distances (Fig. 1–5). The molecules in a solid are arranged in a pattern that is repeated throughout. Because of the small distances between molecules in a solid, the attractive forces of molecules on each other are large and keep the molecules at fixed positions. The molecular spacing in the liquid phase is not much different from that of the solid phase, except the molecules are no longer at fixed positions relative to each other and they can rotate and translate freely. In a liquid, the intermolecular forces are weaker relative to solids, but still strong compared with gases. The distances between molecules generally increase slightly as a solid turns liquid, with water being a notable exception. In the gas phase, the molecules are far apart from each other, and molecular ordering is nonexistent. Gas molecules move about at random, continually colliding with each other and the walls of the container in which they are confined. Particularly at low densities, the intermolecular forces are very small, and collisions are the only mode of interaction between the molecules. Molecules in the gas phase are at a considerably higher energy level than they are in the liquid or solid phase. Therefore, the gas must release a large amount of its energy before it can condense or freeze. Gas and vapor are often used as synonymous words. The vapor phase of a substance is customarily called a gas when it is above the critical temperature. Vapor usually implies that the current phase is not far from a state of condensation. Any practical fluid system consists of a large number of molecules, and the properties of the system naturally depend on the behavior of these molecules. 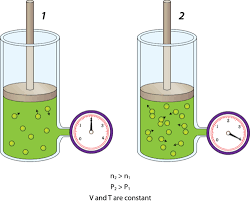For example, the pressure of a gas in a container is the result of momentum transfer between the molecules and the walls of the container. However, one does not need to know the behavior of the gas molecules to determine the pressure in the container. It is sufficient to attach a pressure gage to the container (Fig. 1–6). This macroscopic or classical approach does not require a knowledge of the behavior of individual molecules and provides a direct and easy way to analyze engineering problems. The more elaborate microscopic or statistical approach, based on the average behavior of large groups of individual molecules, is rather involved and is used in this text only in a supporting role.