Skip to main content

Expression for capillary rise and capillary fall - Jurin's law

 

Expression for capillary rise and capillary fall - Jurin's law

Expression for height in Capillary rise
capillary rise

Consider a narrow glass tube of diameter of d dipped in a liquid (say water). Water in the tube will rise above the adjacent liquid level. It is called capillary rise.

Let σ = Surface tension of liquid.
ϴ = Angle of contact between the glass tube and the liquid surface.
h = Height of liquid column in glass tube.

Under equilibrium, two forces are acting on the water inside. The first one is weight of water column and second is the upward force acting on water due to surface tension. The weight of liquid of height h should be balanced by the force at liquid surface. This force at surface of liquid is due to surface tension.

The weight of liquid of height h in the tube = Volume x ρ x g
= (π/4)d2 x h x ρ x g

Here ρ = density of liquid
g = acceleration due to gravity.

The vertical component of surface tensile force = surface tension x circumference x cosϴ
= σ x πd x cosϴ

At equilibrium, the weight of liquid balanced by the vertical component of tensile force.
π/4 d^2 h ρ g= σ πd cosϴ h=(4 σ cosϴ )/ρgd cappillary rise equation

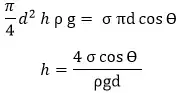
For water and glass tube, the angle ϴ is almost zero. ie cosϴ ≈ 1
Then the equation for capillary rise of water in the glass tube is h = 4 σ /(ρgd)

Expression for Capillary fall

capillary fall

Consider a narrow glass tube dipped in mercury, the level of mercury in tube will be lower than the surface level of mercury outside the tube. It is called capillary depression.
Consider the mercury glass tube arrangement as shown in figure. Two forces are acting on the mercury inside the tube. First one is hydrostatic force that acting upward, and second one is downward force due to surface tension. In equilibrium condition these forces must be equal.

Let h = height of capillary depression.
The hydrostatic force on liquid = Intensity of pressure at depth h x Area
= ρ x g x h x (π/4)d2

Surface tension acting downward = Surface tension x circumference x cosϴ
= σ x πd x cosϴ
Equating two forces, we get
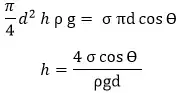
π/4 d^2 h ρ g= σ πd cosϴ h=(4 σ cosϴ )/ρgd capillary fall equation of height

The value of contact angle for mercury in glass tube = 128°

Remember:
👉Capillary is the result of both adhesion and cohesion.
👉Curved free surface of liquid in tube is known as meniscus.
Labels:

Comments

Post a Comment

Popular posts from this blog

Application Areas of Fluid Mechanics

Application Areas of Fluid Mechanics It is important to develop a good understanding of the basic principles of fluid mechanics, since fluid mechanics is widely used both in everyday activities and in the design of modern engineering systems from vacuum cleaners to supersonic aircraft. For example, fluid mechanics plays a vital role in the human body. The heart is constantly pumping blood to all parts of the human body through the arteries and veins, and the lungs are the sites of airflow in alternating directions. All artificial hearts, breathing machines, and dialysis systems are designed using fluid dynamics (Fig. 1–7). An ordinary house is, in some respects, an exhibition hall filled with applications of fluid mechanics. The piping systems for water, natural gas, and sewage for an individual house and the entire city are designed primarily on the basis of fluid mechanics. The same is also true for the piping and ducting network of heating and air-conditioning systems. A refrigera...
2 comments
Read more

THE NO-SLIP CONDITION

 THE NO-SLIP CONDITION Fluid flow is often confined by solid surfaces, and it is important to understand how the presence of solid surfaces affects fluid flow. We know that water in a river cannot flow through large rocks, and must go around them. That is, the water velocity normal to the rock surface must be zero, and water approaching the surface normally comes to a complete stop at the surface. What is not as obvious is that water approaching the rock at any angle also comes to a complete stop at the rock surface, and thus the tangential velocity of water at the surface is also zero. Consider the flow of a fluid in a stationary pipe or over a solid surface that is nonporous (i.e., impermeable to the fluid). All experimental observations indicate that a fluid in motion comes to a complete stop at the surfaceand assumes a zero velocity relative to the surface. That is, a fluid in direct contact with a solid “sticks” to the surface, and there is no slip. This is known as the no-s...
Post a Comment
Read more